Простое приложение в Matlab для прогнозирования
Рассмотрим пример приложения на Matlab, которое осуществляет основные этапы прогнозирования временных рядов с помощью нейронных сетей. Приложение состоит из двух небольших функций, которые рассмотрим подробно далее. Функция Client1
1 function Client1()
a = importdata('GNP.txt')
[b c] = TimeSeries2TrainingSet(a,10,20);
net = newff(b,c,15)
net = train(net,b,c)
p1={[23.1 42.4 49.1 52.7 55.1 60.4 57.5 55.9 62.6 61.3]'}
y=sim(net,p1)
8 end
Строка 1. Заголовок функции. Функция вызывается без параметров ().
Строка 2. С помощью функции Matlab «Importdata» производится считывание из указанного текстового файла 'GNP.txt' временного ряда в матрицу ‘a’.
Строка3. С помощью написанной нами функции «TimeSeries2TrainingSet» вектор a временного ряда преобразуется в обучающее множество нейронной сети в виде матрицы b входных векторов и вектора выходных значений c. При этом нужно указать ширину «скользящего окна» (10) и количество примеров обучающего множества (20). Подробнее функция TimeSeries2TrainingSet будет рассмотрена позже.
Строка 4. С помощью стандартной функции Matlab 'newff' производится построение нейронной сети. В данном варианте вызова функции 'newff' некоторые настроечные параметры не указываются явно и принимают стандартные значения.
Название 'newff' означает, что создается новая сеть прямого распространения (Feed Forward). Такая сеть по умолчанию является двуслойной. При создании сети указываются такие параметры, как обучающее множество b и c, и количество нейронов в скрытом слое (15).
Строка 5. Построенная сеть обучается методом обратного распространения ошибки (Back Propagation)с помощью встроенной функции ‘train'. Как известно, принцип обратного распространения реализован с помощью нескольких конкретных методов. В примере функция ‘train' использует по умолчанию один из наиболее быстрых методов, метод Левенберга-Марквардта. Во время выполнения функции ‘train’ Matlab наглядно демонстрирует процесс и результаты обучения с помощью следующего диалогового окна (Рис.4.1):
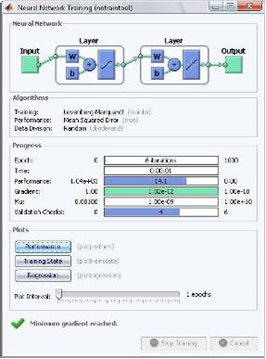
Рис. 4.1. Главное окно, отображающее ход обучения и результаты обучения нейронной сети
Результатом данной функции является обученная сеть, т.е. сеть, в которой веса связей настроены для наилучшего соответствия обучающего множества. Наиболее важным показателем является точность обучения, оцениваемая с помощью MSE-критерия.
Строка 6. Формируется вектор p1, который на следующем шаге будет подаваться на вход сети.
Строка 7. Функция 'sim' позволяет получить с помощью нейронной сети ее выход при заданном входном векторе.
Функция
TimeSeries2TrainingSet
[inputs outputs] = TimeSeries2TrainingSet(timeSeries, winWidth, exampleCount)
% превращает временной ряд с заданной шириной окна winWidth
% в обучающее множество для нейронной сети, состоящее из exampleCount элементов
in=[]=[]n = 1:exampleCount=timeSeries(n:n+winWidth-1)=[in slice']=[out; timeSeries(1,n+winWidth)]=in=out'
Эта функция преобразовывает временной ряд в обучающее множество нейронной сети, используя принцип «скользящего окна». Ее входом является вектор ‘timeSeries’, а выходом - обучающее множество (матрица inputs и вектор outputs).
Заключение
В результате выполнения данной работы удалось получить ряд результатов, в конечном счете позволяющих осуществлять прогнозирование временных рядов.
В первой части работы были рассмотрены основные положения теории прогнозирования. Основной результат - классификация методов прогнозирования и постановка задачи прогнозирования временных рядов. Критерий оценки качества - MSE-критерий.
Во второй части работы рассмотрены основные подходы ИИ, в частности ИНС и ГА. В рамках данной работы в основном используются многослойные сети прямого распространения. Обучение таких сетей предполагается осуществлять с помощью генетического алгоритма с вещественным кодированием.
Рассмотрен классический генетический алгоритм и его модификация (РГА), которая в большей степени подходит для достижения цели работы.
Разработана методика решения задачи прогнозирования временных сетей с помощью сочетания ГА+ИНС, в котором ГА с вещественным кодированием параметров используется как метод обучения многослойной ИНС.
Для практической реализации этой методики спроектированы реализованы программные модули, соответствующие применяемым в рамках работы методам, а также клиентское приложение, позволяющее осуществлять эксперименты с помощью предлагаемой методики.
Для верификации результатов работы разработаны сценарии на языке MATLAB, позволяющие осуществлять сходные эксперименты с помощью встроенных в MATLAB средств.


